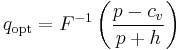Newsvendor model
The newsvendor (or newsboy or single-period[1]) model is a mathematical model in operations management and applied economics used to determine optimal inventory levels. It is (typically) characterized by fixed prices and uncertain demand for a perishable product. If the inventory level is  , each unit of demand above
, each unit of demand above  is lost. This model is also known as the Newsvendor Problem or Newsboy Problem by analogy with the situation faced by a newspaper vendor who must decide how many copies of the day's paper to stock in the face of uncertain demand and knowing that unsold copies will be worthless at the end of the day.
is lost. This model is also known as the Newsvendor Problem or Newsboy Problem by analogy with the situation faced by a newspaper vendor who must decide how many copies of the day's paper to stock in the face of uncertain demand and knowing that unsold copies will be worthless at the end of the day.
Contents |
Profit function
The standard newsvendor profit function is
where  is a random variable with probability distribution
is a random variable with probability distribution  representing demand, each unit is sold for price
representing demand, each unit is sold for price  and purchased for price
and purchased for price  , and
, and  is the expectation operator. The solution to the optimal stocking quantity of the newsvendor which maximizes expected profit is:
is the expectation operator. The solution to the optimal stocking quantity of the newsvendor which maximizes expected profit is:
where 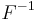 denotes the inverse cumulative distribution function of
denotes the inverse cumulative distribution function of  .
.
Intuitively, this ratio, referred to as the critical fractile, balances the cost of being understocked (a lost sale worth 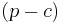 ) and the total costs of being either overstocked or understocked (where the cost of being overstocked is the inventory cost, or
) and the total costs of being either overstocked or understocked (where the cost of being overstocked is the inventory cost, or  so total cost is simply
so total cost is simply  ).
).
Numerical example
Assume that: retail price is 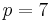 [$/unit] and purchase price is
[$/unit] and purchase price is 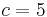 [$/unit]. Furthermore the
[$/unit]. Furthermore the  demand follows a uniform distribution (continuous) between
demand follows a uniform distribution (continuous) between 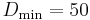 and
and 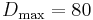 .
.
Therefore optimal inventory level is approximately 59 units.
Extreme situation
If 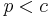 (i.e. the retail price is less than the purchase price), the numerator becomes negative. In this situation, it isn't worth keeping any item in the inventory.
(i.e. the retail price is less than the purchase price), the numerator becomes negative. In this situation, it isn't worth keeping any item in the inventory.
Cost based optimization of inventory level
Assuming that the 'newsvendor' is in fact a small company who wants to produce goods to an uncertain market. In this more general situation the cost function of the newsvendor (company) can be formulated in the following manner:
where the individual parameters are the following:
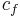 – fixed cost. This cost always exists when the production of a series is started. [$/production]
– fixed cost. This cost always exists when the production of a series is started. [$/production]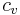 – variable cost. This cost type expresses the production cost of one product. [$/product]
– variable cost. This cost type expresses the production cost of one product. [$/product] – The product quantity in the inventory. The decision of the inventory control policy concerns the product quantity in the inventory after the product decision. This parameter includes the initial inventory as well. If nothing is produced, then this quantity is equal to the initial quantity, i.e. concerning the existing inventory.
– The product quantity in the inventory. The decision of the inventory control policy concerns the product quantity in the inventory after the product decision. This parameter includes the initial inventory as well. If nothing is produced, then this quantity is equal to the initial quantity, i.e. concerning the existing inventory. – Initial inventory level. We assume that the supplier possesses
– Initial inventory level. We assume that the supplier possesses  products in the inventory at the beginning of the demand of the delivery period.
products in the inventory at the beginning of the demand of the delivery period. – penalty cost (or back order cost). If there is less raw material in the inventory than needed to satisfy the demands, this is the penalty cost of the unsatisfied orders. [$/product]
– penalty cost (or back order cost). If there is less raw material in the inventory than needed to satisfy the demands, this is the penalty cost of the unsatisfied orders. [$/product]![E[D]](/2012-wikipedia_en_all_nopic_01_2012/I/c85bd9f5709dd45e6ca2c33ba26e60fa.png) – Expected value of the
– Expected value of the  stochastic variable.
stochastic variable. – This means the demand from the receiver for the product, which is an optional probability variable. [unit]
– This means the demand from the receiver for the product, which is an optional probability variable. [unit] – inventory and stock holding cost. [$ / product]
– inventory and stock holding cost. [$ / product]
On the basis of the cost function the determination of the optimal inventory level is a minimization problem. So in the long run the amount of cost-optimal end-product can be calculated on the basis of the following relation:[1]
See also
References
Further reading
- Ayhan, Hayriye, Dai, Jim, Foley, R. D., Wu, Joe, 2004: Newsvendor Notes, ISyE 3232 Stochastic Manufacturing & Service Systems.
![\pi =E\left[p\min (q,D)\right]-cq](/2012-wikipedia_en_all_nopic_01_2012/I/7cea50f44972598788e39e1b8c89b9a4.png)
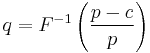
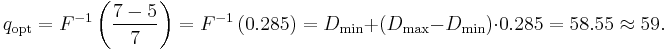
![K(q) = c_f %2B c_v (q-x) %2B p E\left[\max(D-q,0)\right] %2B h E\left[\max(q-D,0)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/b7843ce16370649b194cb70aec02ca3c.png)